Random Ivy Cube information for no reason (this is the Ivy Cube:
There are 3^4 * 6! = 58320 possible states the Ivy Cube can be in, but half of these are impossible due to parity, so there are only 29160 possible scrambles.
Any scramble can be solved within 8 moves, or 12 if you only allow clockwise moves. Of the 29160 possible scrambles:
- 1 takes 0 moves to solve (the solved scramble)
- 8 take 1 move to solve
- 48 take 2 moves to solve
- 288 take 3 moves to solve
- 1640 take 4 moves to solve
- 7582 take 5 moves to solve
- 15262 take 6 moves to solve
- 4221 take 7 moves to solve
- 110 take 8 moves to solve
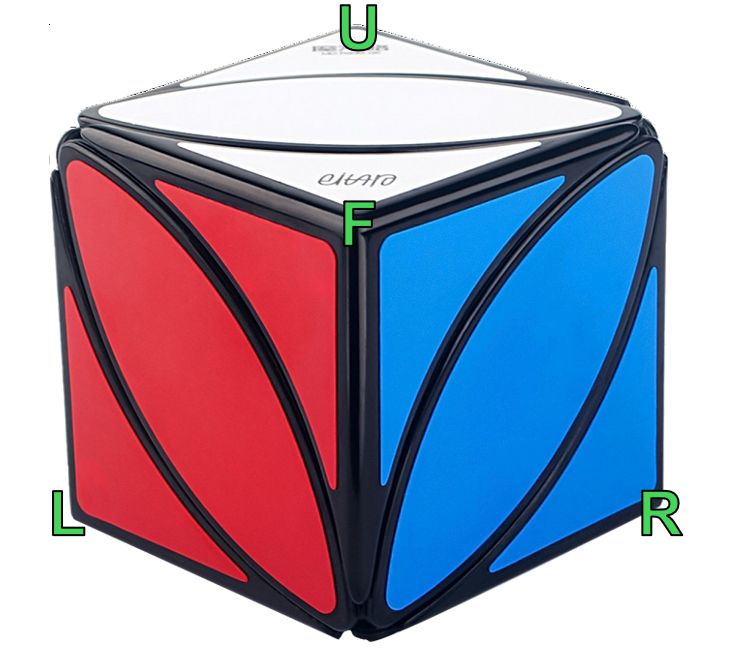
The 110 8-move scrambles are as follows: (see image below for what the letters mean, as with normal rubik's cube notation no apostrophe means a clockwise turn and apostrophe means a counterclockwise turn)
There are 3^4 * 6! = 58320 possible states the Ivy Cube can be in, but half of these are impossible due to parity, so there are only 29160 possible scrambles.
Any scramble can be solved within 8 moves, or 12 if you only allow clockwise moves. Of the 29160 possible scrambles:
- 1 takes 0 moves to solve (the solved scramble)
- 8 take 1 move to solve
- 48 take 2 moves to solve
- 288 take 3 moves to solve
- 1640 take 4 moves to solve
- 7582 take 5 moves to solve
- 15262 take 6 moves to solve
- 4221 take 7 moves to solve
- 110 take 8 moves to solve
The 110 8-move scrambles are as follows: (see image below for what the letters mean, as with normal rubik's cube notation no apostrophe means a clockwise turn and apostrophe means a counterclockwise turn)
F U F U L U F L'
F U F U F' R' U' R'
F U F U L' U F L
F U F R F U R' U
F U F R F R U' R
F U F L U F U L'
F U F L U' L F L
F U F L U' L' U' L'
F U F U' L' F' R U'
F U F U' L' F' R' U'
F U F R' F U R U
F U F R' U F U R
F U F R' L U' R' U
F U F R' L U' R' U'
F U F R' F' L' U R'
F U F L' U R' F' R'
F U R F U F R' U
F U R F U L F' U'
F U R F U L' R L'
F U R F R U L U'
F U R F R U' F R
F U R F L U R L
F U R F R' F' L R
F U R F R' F' L' R'
F U R U F U F R'
F U R U F' R U R
F U R L F U R L
F U R L F R F' R'
F U R L F R' F' R'
F U R L U F L F'
F U R L F' U' L' R'
F U R L F' L' U' R'
F U R L U' R L U
F U R L R' L' F' U'
F U R F' R U R U
F U R F' L R' L' U'
F U R F' U' F U' L
F U R F' U' L' F' U
F U R F' R' F' R L
F U R F' R' F' R' L
F U R F' L' U' R' L
F U R U' L R' F' L'
F U R U' F' L R' L'
F U R L' F L' U' F'
F U R L' U' R F U'
F U R L' U' R U' L'
F U R L' U' R' F' L
F U R L' R' F' L U'
F U L F R U L R
F U L R F L R F'
F U L R F' L' R' U'
F U L R U' R' U' R
F U L R U' L' F' R'
F U L R L' R' F' U'
F U L F' U F R U'
F U L F' L U F' R'
F U L F' L R' U' F'
F U L U' R' F' U' F
F U L R' L' F R' L'
F U F' L R U' R' L'
F U F' U' L F' U R'
F U F' R' L U' L' R
F U F' R' U' L' F' U
F U F' R' L' U' R L
F U R' U F U F R
F U R' U R L' U' R
F U R' L' U F L' R'
F U L' F U F L U
F U L' F U F' R' L'
F U L' F L R L F'
F U L' U F L F U
F U L' U R' F' L' F
F U L' F' U F' L' R
F U L' F' L R U' R'
F U L' R' F R' L' R
F R F U R F R U'
F R F U R' U' R' U'
F R F L F R L' R
F R F R' U' F' L R'
F R U R U F' U R
F R U F' L R' U' L'
F R L F L R U R'
F R L U F L' F' L'
F R L U F' U' R' L'
F R L U R' L U R
F R L F' R' F R' U
F R L F' R' U' F' R
F R L U' F U' R' F'
F R F' R' U F' R L'
F R F' L' R' U' F' R
F R U' R F U F R
F R U' R L' F' U' F
F R L' R F R F L
F R L' U' R F U' L'
F L F R L F L R'
F L F L' R' F' U L'
F L F' L' R F' L U'
F L U' R' L F R' U'
F U' F L' U F' U R'
F U' R U L' R F' U'
F U' R F' R L' F R'
F R' U R' L U' R U'
U F L R' U R' F' U'
U R F L' R' F R' L'
U R U' R' L U' R F'
U L U L' F' U' R L'
F' U F L' U R' F' R'
F' U L R F L R F'
F' U L' F U F' R' L'
F' U' R U L' R F' U'
Comments
-
Next thing I want to try is finding one for
Given how few scrambles there are, it should be easily writable, especially considering another puzzle with the exact same amount of scrambles also had its own algorithm found

< FU > has 15 elements, 30 positions are reached
< F, U > has 540 elements, so can be partitioned into 18 parts. Not entirely sure how you'd be breadth first searching for combinations of these cycles, but I can see how you'd combine parts together.
< F, U, R > has 9720 elements, so is partitioned into another 18 parts (left cosets with < F, U > subgroup but this is Darflen, why talk like I know group theory).
Once that's done, < F, U, R, L > is the whole 29160 permutations, which only splits into 3 parts. Literally just 3. I have a very specific idea on how I'm going to approach this phase.